引文信息:
Mohammad H. Nadimi-Shahraki.An Effective Hybridization of Quantum-based Avian Navigation and Bonobo Optimizers to Solve Numerical and Mechanical Engineering Problems. Journal of Bionic Engineering,2023,20(3),1361–1385.
An Effective Hybridization of Quantum-based Avian Navigation and Bonobo Optimizers to Solve Numerical and Mechanical Engineering Problems
Mohammad H. Nadimi-Shahraki
1 Faculty of Computer Engineering, Najafabad Branch, Islamic Azad University, Najafabad, 8514143131, Iran
2 Big Data Research Center, Najafabad Branch, Islamic Azad University, Najafabad, 8514143131, Iran
Abstract
Hybrid metaheuristic algorithms play a prominent role in improving algorithms' searchability by combining each algorithm's advantages and minimizing any substantial shortcomings. The Quantum-based Avian Navigation Optimizer Algorithm (QANA) is a recent metaheuristic algorithm inspired by the navigation behavior of migratory birds. Different experimental results show that QANA is a competitive and applicable algorithm in different optimization fields. However, it suffers from shortcomings such as low solution quality and premature convergence when tackling some complex problems. Therefore, instead of proposing a new algorithm to solve these weaknesses, we use the advantages of the bonobo optimizer to improve global search capability and mitigate premature convergence of the original QANA. The effectiveness of the proposed Hybrid Quantum-based Avian Navigation Optimizer Algorithm (HQANA) is assessed on 29 test functions of the CEC 2018 benchmark test suite with different dimensions, 30, 50, and 100. The results are then statistically investigated by the Friedman test and compared with the results of eight well-known optimization algorithms, including PSO, KH, GWO, WOA, CSA, HOA, BO, and QANA. Ultimately, five constrained engineering optimization problems from the latest test suite, CEC 2020 are used to assess the applicability of HQANA to solve complex real-world engineering optimization problems. The experimental and statistical findings prove that the proposed HQANA algorithm is superior to the comparative algorithms.
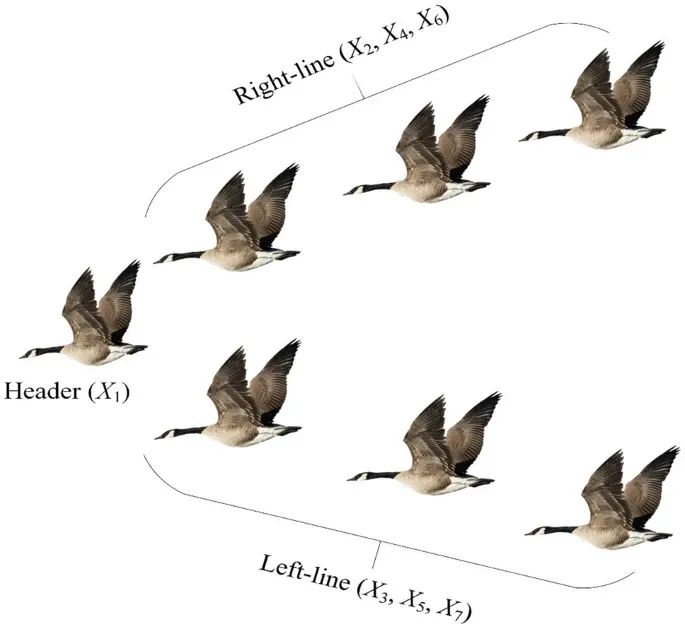
Fig. W1 The V-shaped formation consists of a Header (H), Left-line (L), and Right-line(R).
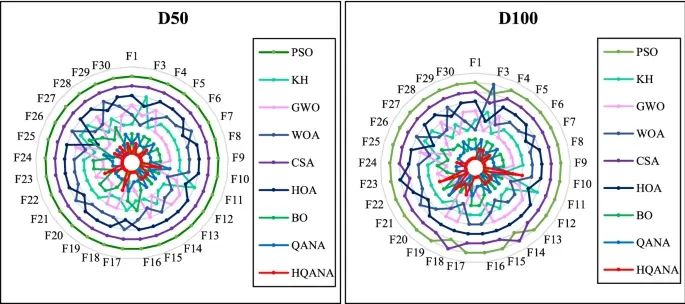
radar graphs and bar charts of algorithms in different dimensions.
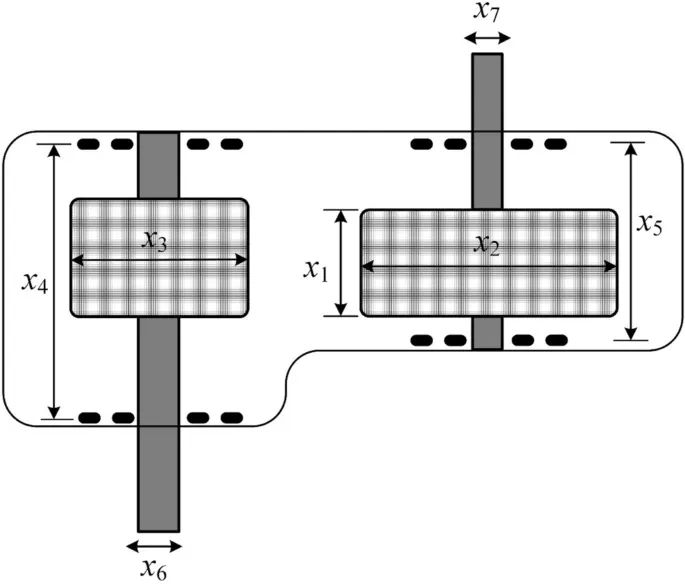
Fig. W3 The schematic of the speed reducer design problem.
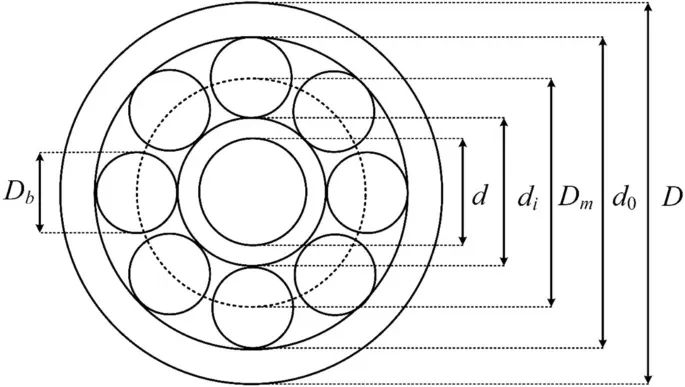
Fig. W4 The schematic of the rolling element bearing design problem.
以上文章转载于微信公众号国际仿生工程学会,如有侵权,请及时联系我们修改或进行删除。
Information Publisher: Mohammad H. Nadimi-Shahraki
Information Release Unit: Faculty of Computer Engineering, Najafabad Branch, Islamic Azad University
Information Source: https://rdcu.be/daeR7

